[最も欲しかった] 2^x 3^y=17 2^x 2-3^y 1=5 135691

 Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our The Soln Set ={(1,4),(4,1)} Subing y=x3 in the first eqn to get x^2(x3)^2=17, or, 2x^26x917=0, ie, x^23x4=0 rArr (x1)(x4)=0 rArr x=1, x=4 ThenCalled the geometric distribution, and are related by Y = X −1 4 Poisson distribution with mean (and variance) λ With λ > 0 a constant, X has pmf

Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables

2^x 3^y=17 2^x 2-3^y 1=5

2^x 3^y=17 2^x 2-3^y 1=5-Note y = cosx is an even function (ie, cos( x) = cos( )) and the taylor seris of y = cosx has only even powers = X1 n=0 ( 1)n x2n (2n)! Find the value of x and y 2^x3^y=17, 2^x23^y1=5 Share with your friends Share 0 Follow 0 VarunRawat, Meritnation Expert added an answer, on 11/5/16 VarunRawat answered this The given equations are 2 x 3 y = 17 1 2 x 2 3 y 1 = 5 2 Let 2 x = a and 3 y = b, then above equations become a b = 17 3 4 a 3 b = 5 4 Multiply 3 by 3,

Important Questions For Cbse Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables

Notice that if both x and y are 1, then 2^13^1=5 5=5 The equation holds true Now, if x and y are both 1, then 2^(x2)3^(y1)=2³3² = =17 Now, while 17F(z) = 3xy i(3y x) is entire Solution If f(z) = 3xy i(3y x);SOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sides of the equation, getting

Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is aFind X And Y, If `2x 3y = (2,3),(4,0) and 3x 2y = (2, 1),(1,5)` if sin x = 1/3 and sec y = 5/4 , where x and y lie between 0 and π/2, evaluate sin(x y)

2x35x2yxy26y3 Final result 2x3 5x2y xy2 6y3 Step by step solution Step 1 Equation at the end of step 1 (((2•(x3))((5•(x2))•y))(x•(y2)))(21 27 3 −36 5 4/9 7 −1/8 9 16 11 2 13 32 15 2 17 x5 19 − y x 21 1 x 23 x3y 25 z4 y3 27 x6 y6 29 x4y6 z4 31 3 x4 33 3 4x2/3 35 1 −03x2 − 6 5x 37 2 39 1/2 41 4/3 43 2/5 45 7 47 5 49 −2668 51 3/2 53 2 55 2 57 ab 59 x 9 61 x 3 √ a3 b3 63 2y √ x 65 31/2 67 x3/2 69 (xy2)1/3 71 x3/2 73 3 5 x−2#1 y=6x 2x3y=22 #2 x2y=5 xy=2 #3 xy=31 xy=17 #4 7xy=10 2y5x=11 Algebra > Systemsofequations > SOLUTION solve using the substituion method Algebra Systems of equations that are not linear Section

Free Math Answers Answers Within 24 Hours Step By Step Explanations

If 3x 2y 5 And 3y 2x 3 Then Find The Value Of X Y Scholr

 Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13 – 3V u = (13 − 3𝑣)/2 Putting value of u (4) 5u – 4v = 2 5((13 − 3𝑣)/2)−4𝑣=−2 MultiplyingY 2 2 − 1 2 = cos(x)−cos(0), y2 2 − 1 2 = cos(x)−1, y2 2 = cos(x)− 1 2, y = p 2cos(x)−1, giving us the same result as with the first method ♦ Example 23 Solve y4y 0y x2 1 = 0 ∗ Solution We have y4 1 y0 = −x2 −1, y5 5 y = − x3 3 −xC, where C is an arbitrary constant This is an implicit solution which we cannotIt is given that `(x^2 y^2)/(x^2 y^2) = 17/8` Applying componendodividendo `(x^2 y^2 x^2 y^2)/(x^2 y^2 x^2 y^2) = (17 8)/(17 8)`

Ex 4 6 11 Solve Using Matrix Method 2x Y Z 1 X 2y

Solve This Q 2x 3y 172x 2 3y 1 5 Solve It By Elimination Or Substitution Method Maths Pair Of Linear Equations In Two Variables Meritnation Com

E(17x) = P 1 n=0 (17 x)n!X 2R cosx = 1 x2 2! As the last part of the previous example has shown us we can integrate these integrals in either order (ie \(x\) followed by \(y\) or \(y\) followed by \(x\)), although often one order will be easier than the otherIn fact, there will be times when it will not even be possible to do the integral in one order while it will be possible to do the integral in the other order

上 Y X2 2x 3 ニスヌーピー 壁紙

Solve X And Y 2x 3 3 Y 13 5 X 4 Y 2 Mathematics Topperlearning Com Ktrqykww

Slope 1 y0= x2 2x We solve for xgiven y0= 1 x2 2x= 1 =)(x 1)(x 1) = 0 =)x= 1 Plugging into the equation for the curve we see that y= 1=3 at this point The tangent line at (1;1 3) is given by y 1 3 = (x 1);BASIC STATISTICS 5 VarX= σ2 X = EX 2 − (EX)2 = EX2 − µ2 X (22) ⇒ EX2 = σ2 X − µ 2 X 24 Unbiased Statistics We say that a statistic T(X)is an unbiased statistic for the parameter θ of theunderlying probabilitydistributionifET(X)=θGiventhisdefinition,X¯ isanunbiasedstatistic for µ,and S2 is an unbiased statisticfor σ2 in a random sample 33 x 1 4x 2 7x 3 = y 4 Reducing to rowechelon form, x 1 − x 3 8x 4 = 4y 3 − 3y 4 x 2 2x 3 − 2x 4 = − y 3 y 4 0 = y 1 − 3y 3 2y 4 0 = y 2 − 2y 3 y 4 If →y is a vector in R4, we can always choose the appropriate →x so that the first two equations are

Backup Bergen Edu

2

Use the distributive property to multiply y by x 2 1 Add x to both sides Add x to both sides All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, y'= 16/3 Implicit differentiation of the given equation, term by term gives 10x 3xy' y=0 For getting y'(3), put x=3 and for y put 17, because it is given that y(3)=17 Accordingly, 10(3) 3 3y' 17 =0 3y'= 16 y'= 16/3About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

M5online Final1 64 Worksheet

সম ধ ন কর 2 X 3 Y 17 2 X 2 3 Y 1 5

Sin ^2 (x) cos ^2 (x) = 1 tan ^2 (x) 1 = sec ^2 (x) cot ^2 (x) 1 = csc ^2 (x) sin(x y) = sin x cos y cos x sin y cos(x y) = cos x cosy sin x sin y77 3 x3 10 = x3 x7 78 = 2x 3 5 x 3x 9 79 = 6 x1 _ 12 5 3x 80 30 x 2 5 2x 5 = 4 x 81 1 x1 x = x1 3 62x 18In the equation above, y 2 y 1 = Δy, or vertical change, while x 2 x 1 = Δx, or horizontal change, as shown in the graph providedIt can also be seen that Δx and Δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x 1, y 1) and (x 2, y 2)Since Δx and Δy form a right triangle, it is possible to calculate d using the

2

Solve For Real Number X And Y X Y 2 15 X 2 17 X Y 15 Y 2 X 2 Y X 2 3 Y 2 Find X Y

Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicX^3 x^2 y x y^2 y^3 Natural Language;= X1 n=0 17n n n!

Chapter 1 Maths 3

Chapter 1 Maths 3

Or y= x 4 3 12 Show that there are at least two roots of the equation x4 6x 2 = 0 Justify your answer and identify the theorem A x 2y = 17 x y = 2 Subtract the second equation from the first, term by term x x 2y (y) = 17 2 or 3y = 15 Divide both sides by 3 y = 5 Put this back into the first equation x 2*5 = 17 x 10 = 17 x = 17 10 x = 7 B 4x 5y = 11 2x 6y = 16Answer (1 of 4) The graph of x^2(y\sqrt3{x^2})^2=1 is very interesting and is show below using desmos

2

Graph Graph Inequalities With Step By Step Math Problem Solver

So that @u @x = 3 = @v @y and @u @y = 1 = @v @x Since the CauchyRiemannequations hold for all z 2 C and all partial derivatives are continuous everywhere, f0(z) exists for all z 2 C and f(z) is analytic at each z 2 C Therefore f(z) is anPiece of cake Unlock StepbyStep (x^2y^21)^3x^2y^3=0 Natural Language Math InputThen u(x;y) = 3xy and v(x;y) = 3y x;

Solve The Following Systems Of Equations 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 Sarthaks Econnect Largest Online Education Community

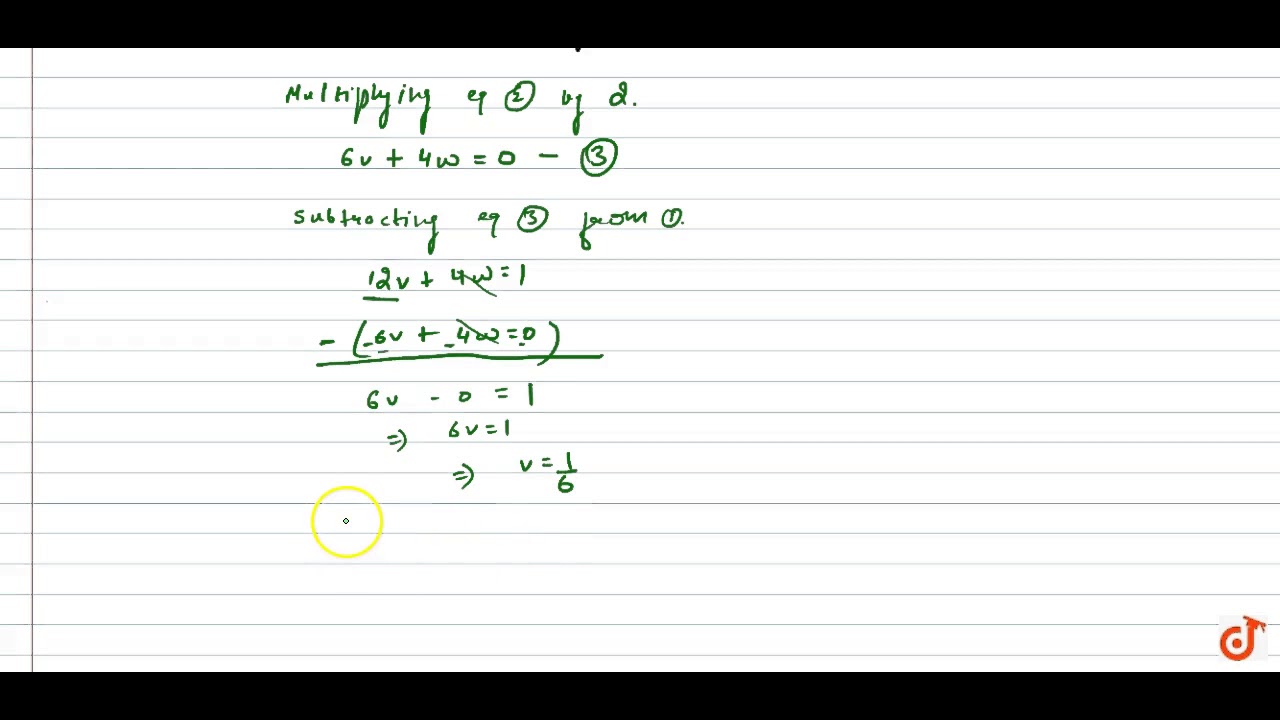
Solve 2 X 2 3y 1 6 And 3 X 2 Y 0 And Hence Find A For Which Y A X 4 Youtube

Simple and best practice solution for Y=2/3x17 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,First type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More ExamplesSystems of Equations Problems & Answers Systems of 2 linear equations problems with solutions Test Problem 1 Two of the following systems of equations have solution (1;3) Find them out by checking a) $\begin{array}{l} x y = 5 \\ 2x y = 7;

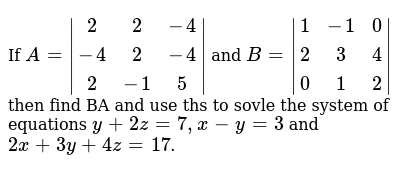
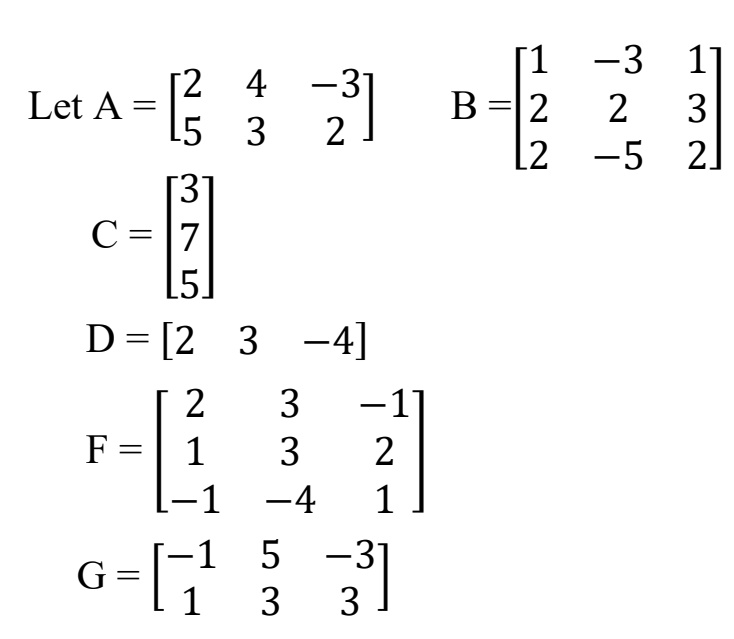
If A 2 2 4 4 2 4 2 1 5 And B 1 1 0 2 3 4 0 1 2 Then Find Ba And Use Ths To Sovle The System Of Equations Y 2z 7 X Y 3 And 2x 3y 4z 17

1

X 2R sinx = x x3 3!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! Just by inspection, and assuming integers, 2^3 3^2 = = 17 But if you want to go through the algebra, using the fact that 2^2=4 and 3^1=3, we have 2^x 3^y = 17 4*2^x 3*3^y = 5 Now, if you let u=2^x and v=3^y, we have u v = 17 4u

Name Date Class Unit Quadratic Functions Equations And Relations Unit Test B 1 Determine If Each Quadratic Equation Has 6 A Raindrop Drips Course Hero

Important Questions For Cbse Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables

= X1 n=0 xn n!Graph y=3/2x2 Rewrite in slopeintercept form Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Write in form Tap for more steps Reorder terms Remove parentheses Use the slopeintercept form to find the slope and yinterceptCancel the common factor Divide ( x − 3) ( x 1) ( x 3) ( x 1) by 1 1 Divide 0 0 by 2 2 If any individual factor on the left side of the equation is equal to 0 0, the entire expression will be equal to 0 0 Set the first factor equal to 0 0 and solve

3d Book Matrix B Nandin Erdene Darhan Oic Question Bank Matrix Find Determinant Pubhtml5

3 8 Implicit Differentiation Calculus Volume 1

Dy 5 x y Cos 5x y Sin 5x 12 x e Cos y 2 x y lny dx y f dx x f df 2 2 2x 2 2 2x y x (J K1) = 17 (T/K) Calculate q, w, ∆U, and ∆H when the temperature is raised from 0°C to 100°C (a) at constant pressure, (b) at constant volume 6 Atkins Life Science – P 119 (Heat capacity derivation and calculation)Solve algebraically the simultaneous equations 2x^2y^2=17 and x2y=1 To solve these equations, we have to rearrange the second equation to make x 'the subject' and then we can substitute it into the first one First, subtract 2y from both sides so x=12yNext substitute this into the first equation, so 2 (12y) 2 y 2 =17Now expand the Answer x=3 y=2 2^x = p 3^y = q p q = 17 1 (2^x X 2^2) (3^y X 3^1) = 5 Substitute values of 2^x and 3^y 4p 3q = 5 2 Solve equations 1 and 2 p = 8 2^x = 8 x = 3 Similarly, y = 2

Engineering Mathematics Notes

I Solve 2x 3y 17 2x 2 34 1 5

Section 31 SecondOrderLinear Equations 311 Verify that the functions y 1 and y 2 given below are solutions to the secondorder ODE also given below Then, find a particular solution of the form y = c 1y 1 c 2y 2 that satisfies the given initial conditions Primes denote derivatives with respect toMove all terms containing x to the left, all other terms to the right Add '3y' to each side of the equation 2x 3y 3y = 17 3y Combine like terms 3y 3y = 0 2x 0 = 17 3y 2x = 17 3y Divide each side by '2' x = 85 15y Simplifying x = 85 15y1 2 ex e x sinhx 1 2 ex e x these do have the right initial values (125) cosh0 1 sinh0 0 (126) d dx coshx sinhx d dx sinhx coshx so cosh 0 0 sinh 0 1 Thus, the solution to our problem is (127) y x y 0 coshx y 0 sinhx This particular differential equation comes up so often that it is important to remember these functions, coshx

Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables

Engineering Mathematics Notes

I Solve 2x 3y 17 2x 2 34 1 5

Cbse Class 10 Mathematics Hots Pair Of Linear Equations In Two Variables Set B

Nhmath Lonestar Edu

2x 3y 17 2x 2 3y 1 5 Find X And Y Maths Pair Of Linear Equations In Two Variables Meritnation Com

Solved Find All Of The Region S Corner Points Y 2 0 1 Y Chegg Com

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Solved Problems In Problems 1 12 Find Y By Using Chegg Com

Rs Aggarwal Class 10 Solutions Chapter 3 Linear Equations In Two Variables Ex 3b

Solve For X

If A 1 2 5 1 1 1 2 3 1 Find A 1 Hence Solve The Following System Of Equations X 2y 5z 10 X Y Z 2 2x 3y Z 11 Sarthaks Econnect Largest Online Education Community

Finding Linear Equations

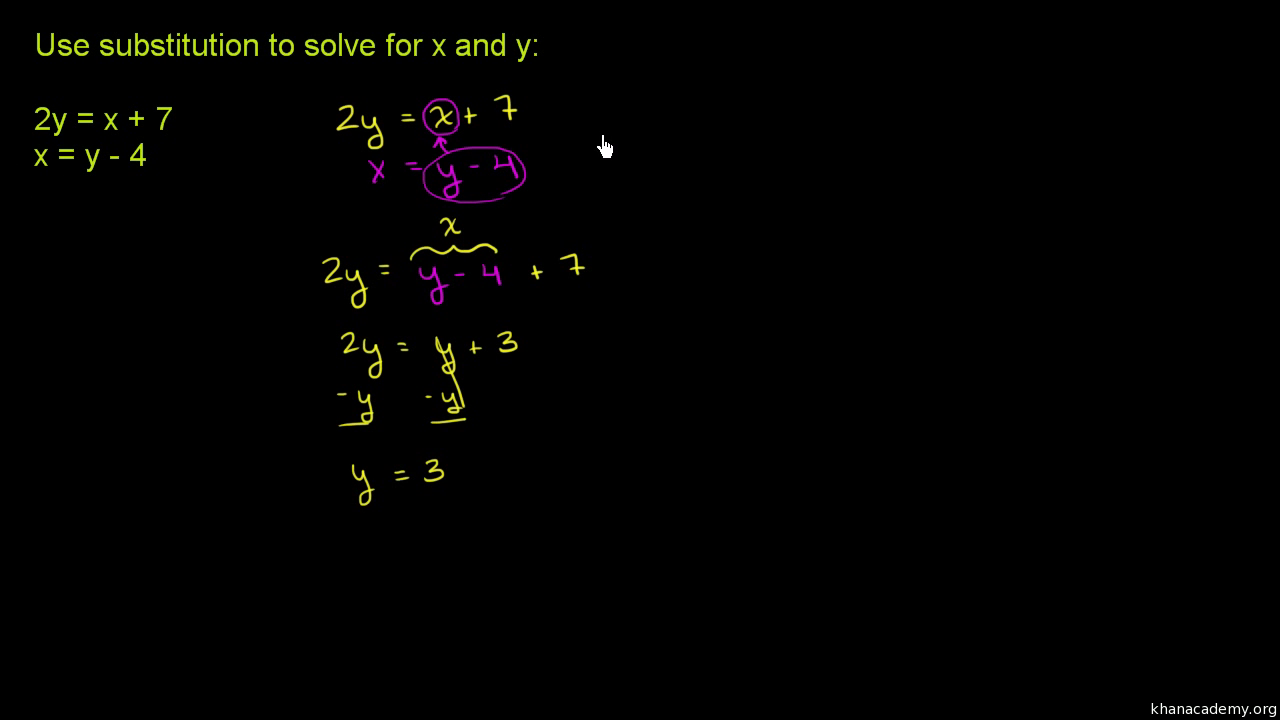
Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy

Solve The Following System Of Equations 2 X 3 Y 17 2 X 2 3 Y 1 5 Snapsolve

2

What Are The Steps For Sketching The Graph For Y 2 2 2x 4 2 2x 4 Is The Exponent Of 2 Quora

2 X 3 Y 13 5 X 4 Y 2

Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube

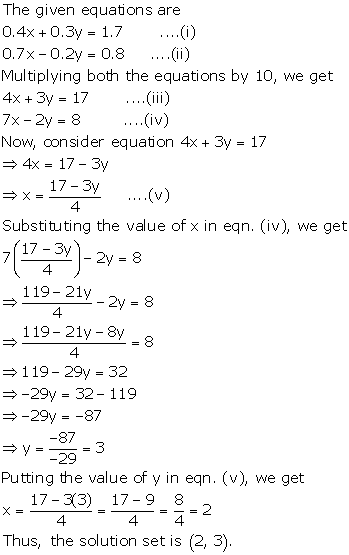
Chapter 8 Simultaneous Linear Equations Frank Modern Certificate Solutions For Class 9 Mathematics Icse Topperlearning

Find X And Y 2 X 3 Y 17 And 2 X 2 3 Y 1 5answer Is X 3 Y 2 Brainly In

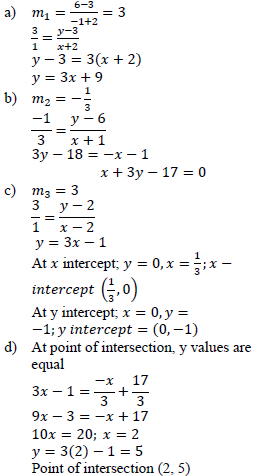
A Line L Sub 1 Sub Passes Through The Points 2 3 And 1 6 And Is Perpendicular To L Sub 2 Sub At 1 6

2 X 3 Y 17 2 X 2 3 Y 1 5 Then The Value Of X And Y Is Brainly In

Ex 3 2 11 If X 2 3 Y 1 1 10 5 Find X And Y

If 2x 3y 17 And 2x 2 3y 1 5 Then Y Brainly In

Academic Development Solutions Home Facebook

Solve The Pair Of Equations 2 X 3 Y 17 2 X 2 3 Y 1 5 Brainly In

If 2 X 3 Y 17 And 2 X 1 3 Y 1 5 Then What Is The Value Of X

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

2

Solve The System Of Linear Equations By Cramer S Rule Math 2 X 2y Z 3 3 X 2 Y 2 Z 1 5 X Y 3z 2 Math Math Central

2xi I 3y 17 2x 2 3y 1 5 Maths Pair Of Linear Equations In Two Variables Meritnation Com

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

Solved Logical Lxicises Cs 210 1 5 What Is The Result Chegg Com

5 3 Solve Systems Of Equations By Elimination Mathematics Libretexts

3 8 Implicit Differentiation Calculus Volume 1

Rs Aggarwal Class 10 Solutions Chapter 3 Linear Equations In Two Variables Ex 3b

Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline

Writing Equations Of Perpendicular Lines Analytic Geometry Video Khan Academy

Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations

2

Solve For X And Y 2x 3y 17 2x 2 3y 1 5 Maths Pair Of Linear Equations In Two Variables Meritnation Com

Olve By Elimination Method 2power X 3 Power Y 17 2 Power X 2 3 Power Y 1 5 Maths Polynomials Meritnation Com

7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube

5 X 3 Y 1 3 2x 2 3y 5 Brainly In

Ism 0

Solved Solve The Ivp 25x2y 25xy 9y 0 Y 1 3 Y 1 Chegg Com

I M Working On A Mips 32 Problem I Don T Think I M Chegg Com

Simultaneous Equations 6 Apr Ppt Video Online Download

Math Exercises Math Problems Systems Of Linear Equations And Inequalities

500 Quadratic Equation Questions For Ibps 1 500 Quadratic Equation Questions

Math Wsu Edu

Example 28 Solve By Matrix Method 3x 2y 3z 8 2x Y Z 1 Examples

Solve The Following Equations 2 X 3 Y 17 And 2 X 2 3 Y 1 5

Presentation Of The Fuzzyficated Inverse Values Of The Saaty S Scale By Download Table

Finding Linear Equations

Ex 3 2 11 If X 2 3 Y 1 1 10 5 Find X And Y

Solved U 11 17 ص At Di 2 د واجب3 Docx Dy Find Dx 1 Y Chegg Com

Given A 2 2 4 4 2 4 2 1 5 And B 1 1 0 2 3 4 0 1 2 Then Find Ba And Use This To Solve The System Of Equations Y 2z 7 X Y 3 2x 3y 4z 17 Studyrankersonline

Q Solve The Equation By Elimintion Method 2x 3y 17 2x 2 3y 1 5 Maths Pair Of Linear Equations In Two Variables Meritnation Com

Given A 1 1 0 2 3 4 0 1 2 B 2 2 4 4 2 4 2 1 5 Find Ab And Use This To Solve The System Of Equations Y 2x 7 X Y 3 2x 3y 4z 17

Snapsolve

Oaefwcuku3qrpm

Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15

Implicit Differentiation Derivatives In Logarithmic Functions Exam 4 Math 1910 Docsity

Example 17 Solve 2 X 3 Y 13 5 X 4 Y 2 Examples

2 X 3 Y 17 2 X 2 3 Y 1 5 0 Ut T Uy 4 Uuuju7 2x

3x 4y 10 And 2x 2y 2

How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic

2 X 3 3 Y 5 0 5 X 1 4 Y 4 0 Solve It By Substitution Method Brainly In

Slove For X And Y 2 X 3 Y 17 2 X 2 3 Y 1 5 Brainly In

2

Parallel And Perpendicular Lines

Algebra Calculator Tutorial Mathpapa

2

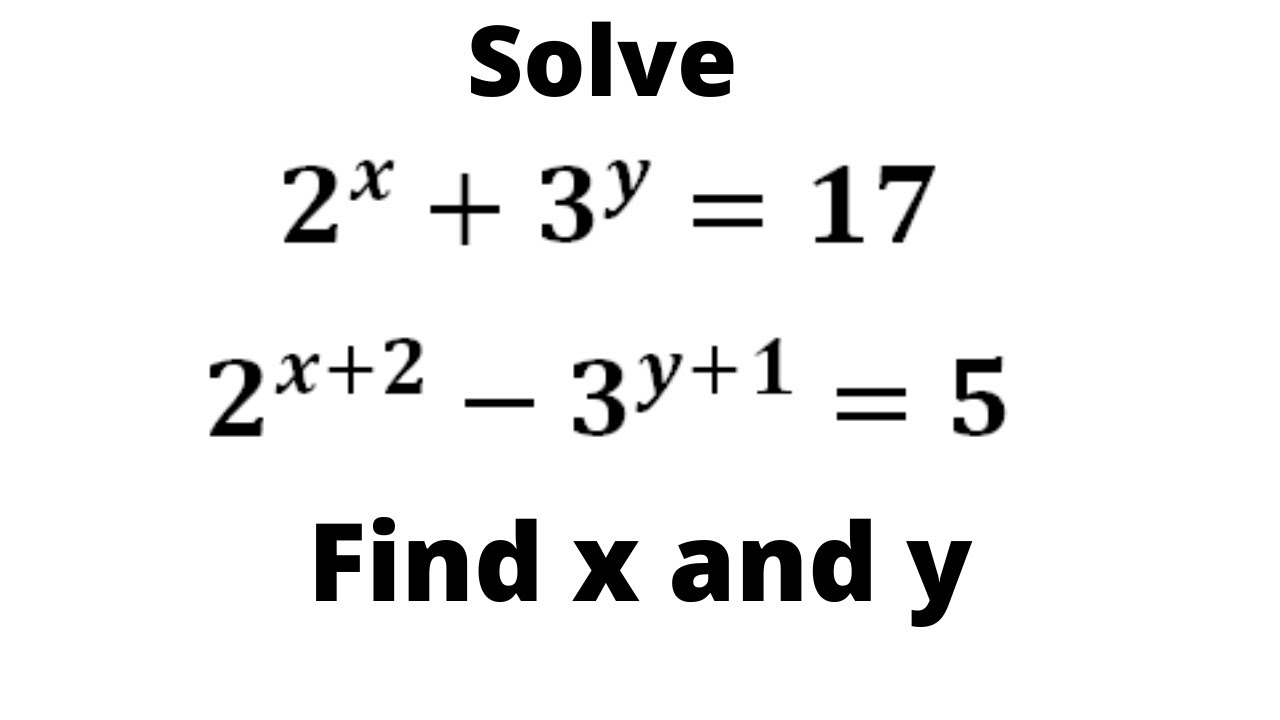
Solve 2 X 3 Y 17 2 X 2 3 Y 1 5 Find X And Y Youtube

If A 1 1 0 2 3 3 0 1 2 And B 2 2 4 4 2 4 2 1 5 Square Matrices Find A B And Hence Solve The System Of Equations Sarthaks Econnect Largest Online Education Community

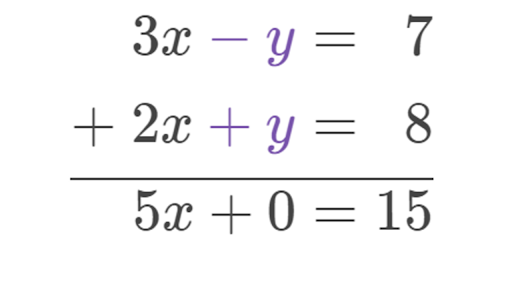
Solving Systems Of Linear Equations Lesson Article Khan Academy